¿Qué es?

La capacidad de procesos es una forma de evaluar qué tan bien un proceso puede producir productos dentro de las especificaciones técnicas establecidas, sin necesidad de ajustes constantes ni milagros de último minuto.

En esencia, responde a la pregunta:

Indicadores clave

Hay varias formas de medir esta capacidad, pero los más conocidos son:

Cp (Índice de Capacidad del Proceso)

Mide la variación del proceso en relación con el ancho de las especificaciones.
Fórmula:

• LS: Límite Superior de Especificación

• LI: Límite Inferior de Especificación

• σ (sigma): Desviación estándar del proceso

Interpretación:

• Cp > 1: el proceso es "capaz"

• Cp < 1: el proceso no es capaz, produce fuera de los límites

• Cp = 1: justito, sin margen de error

Cpk (Índice de Capacidad del Proceso Centrado)

Ajusta el Cp según qué tan centrado está el proceso dentro de los límites.
Fórmula:

Donde μ es la media del proceso.

Interpretación:

• Si Cp ≈ Cpk, el proceso está bien centrado

• Si Cpk < Cp, hay desviación hacia un lado

Son los dos tipos de variación que pueden afectar un proceso:

• Causas comunes :
  Son variaciones naturales e inherentes al sistema. Están presentes constantemente y son difíciles de eliminar individualmente (ej. pequeñas fluctuaciones en materiales o condiciones del entorno).

• Causas especiales:
  Son variaciones no habituales que aparecen por eventos específicos (ej. fallas de máquina, error humano). Pueden identificarse y corregirse.

Importancia en la capacidad del proceso:
Un proceso que solo presenta causas comunes está en control estadístico y su capacidad se puede evaluar de manera confiable con índices como Cp.
Si hay causas especiales, se debe corregir antes de evaluar la capacidad

El coeficiente de variación es aquel que nos permite medir la variabilidad o dispersión relativa de un conjunto de datos en relación con la media aritmética.

Es especialmente útil porque se trata de una medida adimensional, es decir, no depende de las unidades de medida de los datos, lo que facilita la comparabilidad entre distintos conjuntos de datos o entre diferentes variables económicas y financieras.

El coeficiente de variación nos permite comparar la volatilidad de distintas inversiones financieras, evaluar la consistencia de los resultados obtenidos por diferentes áreas de una empresa o comparar la dispersión de cifras de negocio en distintos periodos o regiones. 

Ejemplo practico: 

Imaginamos que deseamos comparar dos posibles inversiones. La inversión A tiene una media de retorno del 8% y una desviación estándar del 2%, mientras que la inversión B tiene una media de retorno del 10% y una desviación estándar del 5%. A primera vista, parece que la inversión B es más atractiva por su mayor retorno medio, pero analicemos su coeficiente de variación:

• Inversión A: CV = (2 / 8) * 100% = 25%
• Inversión B: CV = (5 / 10) * 100% = 50%

Podemos observar que, pese a un mayor retorno medio, la inversión B tiene un coeficiente de variación superior, lo que indica que es más volátil y, por lo tanto, podría ser considerada como más riesgosa en comparación con la inversión A.

Es un teorema de la estadística que afirma que en cualquier distribución (no necesariamente normal), al menos 1−1k21 - \frac{1}{k^2}1−k21​ de los valores estarán dentro de k desviaciones estándar de la media, donde k>1k > 1k>1.

Aplicación en el control de calidad:
Se utiliza como una garantía mínima de dispersión, incluso si la distribución de los datos no es normal

• Para k=3k = 3k=3, al menos:

  1−132=1−19=0.888⇒88.89%1 - \frac{1}{3^2} = 1 - \frac{1}{9} = 0.888 \Rightarrow 88.89\%1−321​=1−91​=0.888⇒88.89%

  de los valores estarán dentro de μ±3σ\mu \pm 3\sigmaμ±3σ, independientemente de la forma de la distribución.

Comparación con la distribución normal:
En una distribución normal, se sabe que aproximadamente el 99.73% de los datos están dentro de μ±3σ\mu \pm 3\sigmaμ±3σ.
Sin embargo, la desigualdad de Chebyshev es más conservadora y se usa cuando no se puede asumir normalidad

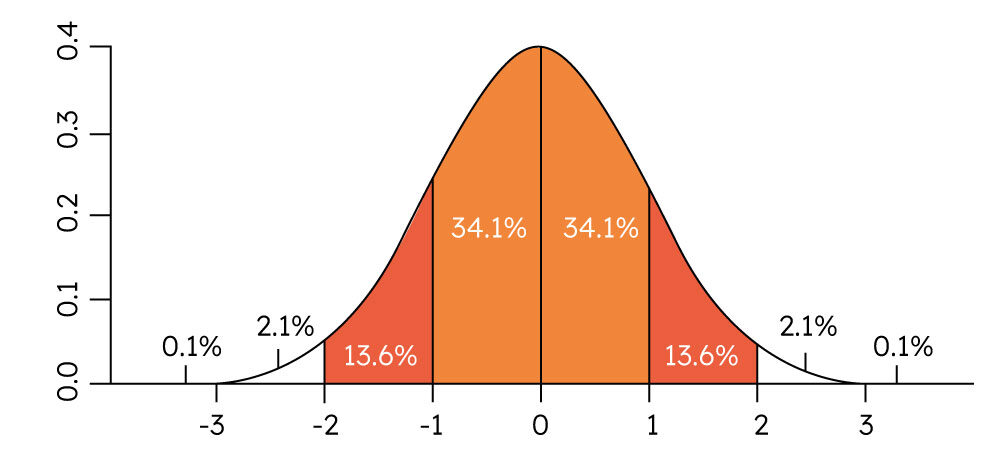
Desviacion Estandar

     La desviación estándar es una medida estadística clave que indica la dispersión de un conjunto de datos respecto a su media. Se calcula determinando primero la media, luego las diferencias de cada valor respecto a ella, elevando al cuadrado dichas diferencias, obteniendo la varianza, y finalmente extrayendo la raíz cuadrada. Una desviación estándar baja indica que los datos están agrupados cerca de la media, mientras que una alta sugiere mayor dispersión. 

     Esta medida es crucial en campos como la ingeniería, economía, psicología y ciencias, ya que evalúa la estabilidad de procesos y la confiabilidad de mediciones. En control de calidad, una baja desviación estándar indica productos similares, y en finanzas, mide la volatilidad del riesgo. También es útil para comparar conjuntos de datos, siendo más consistente aquel con menor desviación estándar. Se expresa en las mismas unidades que los datos, lo que facilita su interpretación.

Una gráfica de desviación estándar, a menudo representada como una curva de campana, ilustra la dispersión de los datos alrededor de la media. 

Es un concepto fundamental en el control estadístico de procesos (SPC) que se refiere a la capacidad de un proceso para operar de manera consistente a lo largo del tiempo, sin la presencia de causas especiales de variación. En otras palabras, un proceso estable es aquel cuyas salidas son previsibles y se mantienen dentro de límites estadísticos normales (límites de control), lo que indica que solo está influenciado por causas comunes (o naturales) de variación, que son inherentes al propio proceso.

Un proceso se considera estable si sus datos se distribuyen de forma aleatoria y están contenidos dentro de los límites de control establecidos en una carta de control. Estos límites no son los mismos que las especificaciones del cliente (USL y LSL), sino que se calculan a partir de la variabilidad del proceso y reflejan su comportamiento interno. Cuando los puntos se mantienen dentro de estos límites sin patrones inusuales, se puede decir que el proceso es predecible y, por lo tanto, estadísticamente controlado.

Si en un proceso aparecen puntos fuera de los límites de control, o se detectan patrones sistemáticos (como tendencias, ciclos o agrupaciones), se sospecha la existencia de causas especiales de variación, lo que indica que el proceso es inestable. En ese caso, se deben identificar y eliminar esas causas para restaurar la estabilidad.

Las gráficas de control de calidad son herramientas estadísticas que permiten monitorear si un proceso se mantiene estable. Un proceso está “en control” cuando solo presenta variaciones comunes, es decir, aquellas que forman parte de su comportamiento normal. Si aparecen variaciones especiales, el proceso se desestabiliza y ya no se puede predecir su resultado. Por eso, estas gráficas ayudan a identificar cuándo intervenir y cuándo dejar que el proceso continúe sin ajustes innecesarios.

Beneficios de las gráficas de control

Las gráficas de control de calidad nos sirven para:

•          Determinar el estado de control de un proceso
•          Diagnosticar el comportamiento de un proceso en el tiempo
•          Indicar si un proceso ha mejorado o ha empeorado
•          Permitir identificar las dos fuentes de variación de un proceso
•           Además, las gráficas de control sirven como herramientas de detección de problemas

Fuentes de variación en un proceso

Causas Asignables o Especiales

• Son los factores esporádicos que desestabilizan el sistema
• Su identificación es inmediata y fácil

Causas Comunes o Naturales

• Son los factores que afectan en poco la variabilidad del sistema
• Su presencia es aleatoria y no son de fácil detección
• Generalmente están relacionadas con aspectos administrativos

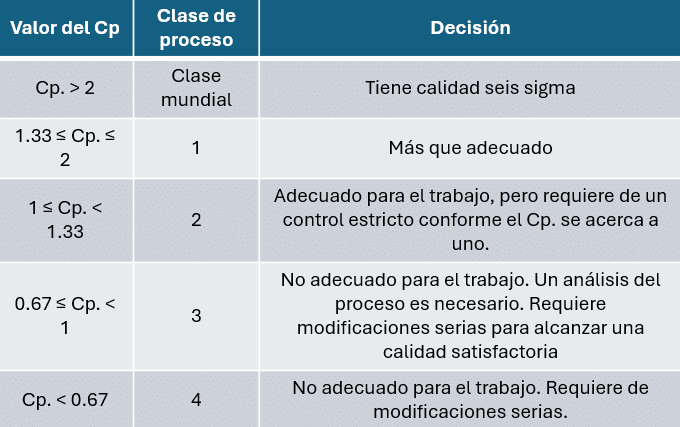
El índice Cp es una métrica utilizada para evaluar la capacidad potencial de un proceso. Este índice mide qué tan capaz es un proceso de cumplir con las especificaciones establecidas, considerando únicamente la variación natural del proceso y sin tomar en cuenta si el proceso está centrado respecto al valor nominal. La fórmula del índice Cp es:

Donde:

• ES  :

  ES Límite superior de especificación.

• EI

    :EI Límite inferior de especificación.

• σ

   : Desviación estándar del proceso.

Interpretación del Índice Cp

• Cp > 1: El proceso es potencialmente capaz de cumplir con las especificaciones, ya que la variación natural del proceso es menor que el rango de tolerancia.
• Cp = 1: El proceso está justo en el límite de cumplir con las especificaciones. Cualquier aumento en la variabilidad podría generar productos fuera de especificación.
• Cp < 1: El proceso no es capaz de cumplir con las especificaciones, ya que su variación natural excede el rango de tolerancia

Limitaciones del Índice Cp

El índice Cp no considera si el proceso está centrado respecto al valor nominal. Por ejemplo, un proceso puede tener un Cp alto pero estar descentrado, lo que significa que una parte significativa de los productos podría estar fuera de los límites de especificación. Para abordar esta limitación, se utiliza el índice Cpk, que incluye el centrado del proceso en su cálculo

¿Qué son?
Los índices Cpi (para la especificación inferior) y Cps (para la especificación superior) son herramientas estadísticas que evalúan la capacidad real de un proceso considerando qué tan cerca está la media del proceso de los límites de especificación.
A diferencia de los otros índices, este sí consideran el centrado del proceso, ya que se calculan usando la media (μ\mu). Esto los hace más precisos cuando el proceso no está perfectamente centrado respecto al valor nominal

FORMULA:

Cpₘ (Índice de Capacidad del Proceso Taguchi) es una medida de la capacidad del proceso que incorpora el objetivo nominal (valor deseado) dentro del análisis de la variabilidad del proceso. A diferencia de Cp o Cpk, que solo consideran los límites de especificación, Cpₘ penaliza la desviación del valor objetivo, alineándose con la filosofía de calidad de Taguchi, que promueve la idea de que cualquier desviación del objetivo representa una pérdida para el cliente.

Ventajas:

• Refleja con mayor precisión la verdadera calidad del producto desde el punto de vista del cliente.

Se alinea con la función de pérdida de Taguchi, la cual considera que toda desviación del objetivo implica una pérdida económica.

Fomenta una cultura de mejora continua más exigente, incentivando procesos más estables y eficientes.

Es ideal para industrias de alta precisión como la médica, aeronáutica y electrónica, donde pequeñas desviaciones pueden ser críticas.

• Es más complejo de calcular que Cp o Cpk, lo que puede dificultar su comprensión y aplicación.

Es menos conocido y usado en la industria, lo que puede generar resistencia a su implementación.

Penaliza incluso desviaciones pequeñas del objetivo, lo que puede parecer excesivo en procesos con tolerancias amplias.