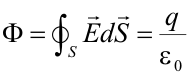En la historia de la física, el "calórico" era una sustancia invisible e inmaterial que, según la teoría del siglo XVIII, se pensaba que fluía de los cuerpos calientes a los fríos y era responsable del calor. La teoría del calórico fue una hipótesis científica que explicó fenómenos térmicos antes de ser reemplazada por la teoría moderna de la energía.

 "Caloric". En: The Oxford Dictionary of Physics. Oxford University Press.https://www.oxfordreference.com/display/10.1093/oi/authority.20110803095543541

Carl Friedrich Gauss (1777-1855) considerado como “príncipe de las matemáticas”, fue un académico con gran influencia en un amplio rango de áreas de las matemáticas y de la ciencia, realizando contribuciones realmente valiosas en teoría de números, análisis matemático, geometría diferencial, estadística, álgebra, geodesia, magnetismo u óptica.

Freire, N. (2024). Carl Friedrich Gauss, el príncipe de las matemáticas. National Geographic España. https://www.nationalgeographic.com.es/ciencia/carl-friedrich-gauss_21953 

Un ciclo termodinámico idealizado que define el rendimiento máximo posible de una máquina térmica operando entre dos temperaturas. Fue formulado por Sadi Carnot y es fundamental en la termodinámica teórica.

Cortadura de dedekind, en matemáticas, particularmente en los sistemas numéricos, en memoria del matemático alemán Richard Dedekind, es un subconjunto especial de cuerpo ordenado, de números racionales. Dichos subconjuntos son usados para construir un cuerpo ordenado completo arquimediano, concretamente los números reales.

EcuRed. (s.f.). Cortadura de Dedekind. Recuperado el 29 de junio de 2025, de https://www.ecured.cu/Cortadura_de_Dedekind

Es la obra más significativa de Carl Friedrich Gauss. En ella reúne los resultados más importantes que se conocían hasta el momento sobre la Teoría de Números, dotándoles de una conexión y dejando de ser un mero conjunto de teoremas y conjeturas sin ninguna convergencia. A su vez, Gauss expuso nuevas investigaciones sobre esta teoría que dieron lugar al libro de mayor trascendencia para todos los grandes matemáticos de la época.

Infantes, A. (2022). Disquisitiones Arithmeticae: Formas binarias cuadráticas y la Teoría Algebraica de Números. Universidad Autónoma de Madrid. https://verso.mat.uam.es/~enrique.gonzalez.jimenez/docencia/TFs/TFG_MAT22_memoria_InfantesSerrano_Andrea.pdf

El pensamiento gaussiano es un enfoque matemático y lógico inspirado en Carl Friedrich Gauss, que se caracteriza por el uso del razonamiento analítico, la búsqueda de patrones, la precisión en los cálculos y la resolución eficiente de problemas complejos mediante métodos sistemáticos y rigurosos.

de Losada, M. F. (1995). El clamor de los beocios y el pensamiento revolucionario de gauss. Boletín de Matemáticas, 1(2), 39-59.

https://revistas.unal.edu.co/index.php/bolma/article/view/18219

Físico y químico británico clave en el desarrollo del electromagnetismo.

Enciclopedia Britannica. (s.f.). Michael Faraday. https://www.britannica.com/biography/Michael-Faraday

Una teoría química del siglo XVII que sostenía que las sustancias combustibles contenían una sustancia invisible llamada "flogisto", que se liberaba durante la combustión. Esta teoría fue utilizada para explicar fenómenos de calcinación y combustión antes de ser refutada por la teoría moderna de la oxidación.

Matemático alemán con gran influencia en la matemática del siglo XIX.

Springer. (2001). Encyclopaedia of Mathematics (Vol. 4). Springer. https://link.springer.com/referencework/10.1007/978-1-55608-010-4

Es la ciencia que se encarga de estudiar medir la forma dimensiones y características del campo gravitatorio de la Tierra utilizando métodos matemáticos físicos astronómicos para determinar con precisión la posición de puntos sobre la superficie terrestre siendo esencial para la elaboración de mapas el funcionamiento del GPS, así como el diseño de obras de ingeniería además permite monitorear fenómenos naturales como terremotos y desplazamientos tectónicos (Rojas, 2023).

Rojas Jaramllo, E. (2023). Aplicaciones de la geodesia en zonas de deslizamiento de laderas https://repositorioinstitucional.buap.mx/server/api/core/bitstreams/96ea3447-3374-4ff5-8e20-0c7caeee01b7/content

Se refiere a cualquier sistema geométrico que no sigue los postulados de la geometría euclidiana, especialmente el quinto postulado sobre las paralelas. En lugar de trabajar en un plano "plano" como en la geometría euclidiana, estas geometrías exploran espacios con diferentes curvaturas.

Vicharelli. D. (2023). Geometría euclidiana y no euclidiana/Similitudes y diferencias. Study.com. https://study.com/academy/lesson/differences-between-euclidean-non-euclidean-geometry.html#:~:text=La%20geometr%C3%ADa%20no%20euclidiana%20es,m%C3%A1s%20de%20una%20l%C3%ADnea%20paralela.

Fue un matemático médico y filósofo italiano del Renacimiento nacido en 1501 en Pavía reconocido por su obra Ars Magna que resolvió ecuaciones cúbicas y cuárticas lo que marcó un avance crucial en el álgebra además pionero en el estudio de la probabilidad realizó investigaciones en la medicina y el juego murió en 1576 dejando un legado significativo en varias disciplinas científicas (Bubello, 2023).

Bubello, J. (2023). Representaciones astrológicas en la autobiografía Liber de libris propris de Girolamo Cardano (1501-1576). In Autobiografía, historia y memoria: Historias de vida como recursos en la enseñanza de la Historia Moderna (pp. 56–67). Universidad Nacional de La Plata; EDULP. https://www.memoria.fahce.unlp.edu.ar/libros/pm.5999/pm.5999.pdf

La Revolución Industrial fue un proceso histórico iniciado en el siglo XVIII en Inglaterra, que marcó el paso de una economía agrícola y artesanal a una industrial y mecanizada. Impulsada por innovaciones como la máquina de vapor, transformó la producción, el transporte y la organización social, dando origen al capitalismo moderno y al crecimiento de las ciudades.

Fernández, L. E. Í. (2012). Breve historia de la Revolución Industrial. Nowtilus.

https://acortar.link/JWXKuW

Fue un destacado matemático y físico suizo del siglo XVIII reconocido por sus contribuciones a las matemáticas y las ciencias trabajando en cálculo teoría de números geometría astronomía mecánica introdujo notaciones como e para la base de los logaritmos naturales e i para la unidad imaginaria su obra tiene más de 800 publicaciones lo que lo convierte en uno de los matemáticos más prolíficos de la historia (Navarro et al., 2024).

Navarro, C. F., Arce, L. C., & Márquez, F. J. C. (2024). biografía de Euler y Gauss como inspiración para estudiar ciencias. Transdigital, 5(9), e338. https://doi.org/10.56162/transdigital338

El flujo del campo eléctrico a través de cualquier superficie cerrada es igual a la carga q contenida dentro de la superficie, dividida por la constante ε0.

Martín, T. y Serrano, A. (s.f.). Flujo del campo eléctrico. Ley de Gauss. Universidad Politécnica de Madrid. https://www2.montes.upm.es/dptos/digfa/cfisica/electro/gauss.html

 Es una matriz cuadrada especial que juega un papel crucial en las operaciones matriciales, actuando como un elemento neutro y siendo fundamental en la definición de matrices inversas. 

Rodó. P. (2024). Matriz identidad: Qué es y para qué se usa en matemáticas. Economipedia. https://economipedia.com/definiciones/matriz-identidad.html#:~:text=Act%C3%BAa%20como%20un%20elemento%20neutro,realizar%20otras%20operaciones%20con%20matrices.

El modelo atómico de Bohr describe al átomo como un núcleo central con protones y neutrones, alrededor del cual los electrones giran en órbitas circulares específicas y cuantizadas, sin emitir energía, pero que pueden saltar entre estas órbitas absorbiendo o emitiendo energía en forma de luz.

Levada, C. L., Maceti, H., Lautenschleguer, I. J., & de Magalhâes Oliveira Levada, M. (2013). Consideraciones sobre el modelo del átomo de Bohr. Revista de la Sociedad Química del Perú, 79(2), 178-184.

http://www.scielo.org.pe/scielo.php?pid=S1810-634X2013000200011&script=sci_arttext&tlng=pt

Los modelos atómicos son representaciones teóricas que explican la estructura interna del átomo, cómo están organizadas sus partículas (electrones, protones y neutrones) y cómo interactúan, evolucionando desde ideas filosóficas hasta teorías científicas basadas en evidencia experimental.

Páez, Y., Rodríguez, M. A., & Niaz, M. (2004). Los modelos atómicos desde la perspectiva de la historia y filosofía de la ciencia: un análisis de la imagen reflejada por los textos de química de bachillerato. Investigación y postgrado, 19(1), 51-77.

https://ve.scielo.org/scielo.php?pid=S1316-00872004000100004&script=sci_arttext

 Son una herramienta matemática que permite ampliar el alcance de las soluciones a ecuaciones y problemas que no pueden ser resueltos utilizando únicamente números reales. 

Freire. N. (2023). Los números imaginarios en el mundo real. National Geographic España. https://www.nationalgeographic.com.es/ciencia/numeros-imaginarios-mundo-real_20834

Son símbolos gráficos que representan ideas, objetos o acciones de forma visual y sencilla, ya que se utilizan para comunicar mensajes de manera rápida y universal, sin necesidad de palabras, además son comunes en señales de tránsito, etiquetas de productos y manuales de instrucciones (Manitio, 2023).

Manitio, G. I. P., & Esteves-Fajardo, Z. I. (2023). Importancia de los pictogramas para el inicio de la prelectura. CIENCIAMATRIA, 9(1), 617–627. https://doi.org/10.35381/cm.v9i1.1089

También conocido como el quinto postulado de Euclides, afirma que por un punto exterior a una recta dada, solo se puede trazar una única línea paralela a la recta original. Este postulado es fundamental en la geometría euclidiana.

Girme. G. (2023). Postulado de las Paralelas de Euclides/ Definición y ejemplos. Study.com.https://study.com/academy/lesson/the-parallel-postulate-and-indirect-proof.html#:~:text=El%20postulado%20de%20las%20paralelas%20establece%20que%20si%20una%20l%C3%ADnea,sumen%20menos%20de%20180%20grados.

Fue un matemático e ingeniero italiano nacido en 1526 en Bolonia es conocido por su obra L'Algebra donde introdujo los números complejos y sus aplicaciones en la resolución de ecuaciones cúbicas Bombelli falleció en 1572 dejando un legado importante en las matemáticas del renacimiento (Gavagna, 2022).

Gavagna, V. (2022). Due protagonisti bolognesi dell’algebra rinascimentale: Ludovico Ferrari e Rafael Bombelli. In Matematica, Cultura E Societa (Vols. 7–3, pp. 249–265). https://flore.unifi.it/bitstream/2158/1301519/1/Gavagna%20RUMI%20Dicembre%202022.pdf

La regla de Cramer es un método que permite calcular la solución de un sistema con “n” ecuaciones y “n” incógnitas, siempre y cuando el determinante de la matriz asociada “A” sea diferente a cero.

De la Rosa, A., Luna, J., Minjares, M., Rivera, S., Rodríguez, A. y Sánchez, G. (2017). Regla de Cramer. En Matemáticas I (Álgebra Lineal). Licenciatura en Contaduría [CD-ROM]. México: UNAM. https://repositorio-uapa.cuaed.unam.mx/repositorio/moodle/pluginfile.php/2603/mod_resource/content/1/UAPA-Regla-Cramer/index.html#introduccion

La teoría de la relatividad, formulada por Albert Einstein a inicios del siglo XX, revolucionó la física al explicar cómo el tiempo y el espacio se relacionan con la velocidad y la gravedad.

Einstein, A. (2001). Relativity: The special and the general theory (R. W. Lawson, Trans.). Routledge. (Trabajo original publicado en 1916)